Критерий Коши для функции в окрестности точки. Теорема об эквивалентности критерия существованию предела у функции

Def.

Функция y = f(x), определённая в окрестности (a), удовлетворяет условию Коши, если

∀ ε > 0 ∃ δ_ε: 0 < δ_ε< θ: ∀ x′, x″ ∈ 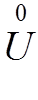_δ(a) → |f(x′) − f(x″)| < ε

Теорема 7

Для того, чтобы функция y = f(x), определённая в окрестности (a), удовлетворяла критерию Коши необходимо и достаточно, чтобы она имела предел в точке a.

Доказательство

Пусть критерий выполнен и {x_n} произвольная последовательность, для которой Тогда {f(x_n)} удовлетворяет критерию Коши для последовательностей и Если для другой посл. {x′_n} то A = B, т. к. в противном для посл. {x″_n} = {x_n}∪{x′_n} предела {f(x″_n)} нет.

Пусть

Тогда

∀ ε > 0 ∃ δ_ε: 0 < δ_ε < θ: ∀ x′, x″ ∈ 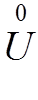_δ(a) → |f(x′) − A| < 0,5ε, |f(x″) − A| < 0,5ε

|f(x′) − f(x″)| = |f(x′) − A − (f(x″) − A)| ≤ |f(x′) − A| + |f(x″) − A| < ε