Равномерная непрерывность функции на множестве. Теорема о равномерной непрерывности функции на отрезке

Def.

Функция y = f(x) равномерно непрерывна на множестве Х:

∀ ε > 0 ∃ δ = δ_ε: ∀ x₁, x₂ ∈ X: |x₁ − x₂| < δ → |f(x₁) − f(x₂)| < ε

Пример 3

Функция y = x² непрерывна на множестве X = [0; +∞), но не равномерно непрерывна на нём и равномерно непрерывна на отрезке X = [0; 1].

Доказательство

X = [0; +∞)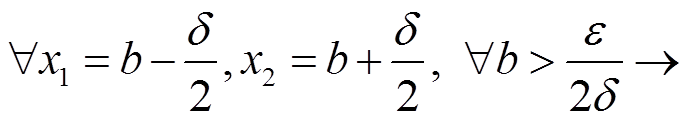

|x₁² − x₂²| = |x₁ − x₂|(x₁ + x₂) = δ·2b > ε

Если X = [0; 1], то δ = . Тогда |x₁² − x₂²| = |x₁ − x₂| · |x₁ + x₂| < ·2 = ε