Равномерная непрерывность функции на множестве. Теорема о равномерной непрерывности функции на отрезке
Теорема 6
Всякая непрерывная на отрезке функция равномерно непрерывна на этом отрезке.
Доказательство
От противного: ∀ 
> 0: ∀ δ = 
∃ xn′, xn″∈[a; b]: |xn′ − xn″| < → |f(xn′) − f(xn″)| ≥ .
Из ограниченности последовательностей
Из непрерывности функции в точке x = x0 → ∃ K
∀ k > K → |f(x′nk) − f(x0)| <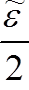 
, |f(x″nk) − f(x0)| < →
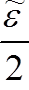|f(x′nk) − f(x″nk)| ≤ |f(x′nk) − f(x0)| + |f(x0) + f(x″nk)| <
Противоречиe
13/17
