Равномерная сходимость функциональной последовательности

Def.

Функция 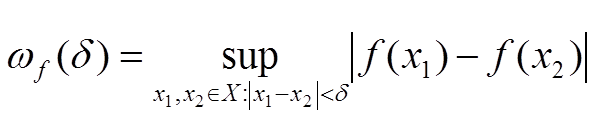переменной δ > 0 называется колебанием функции y = f(x) на множестве X.

В примере 3 для X = [0; +∞), ω_f (δ) = ∞

                    для X = [0; 1], ω_f (δ) ≤ 2δ

Функция равномерно непрерывна на множестве X, если .

Вопрос

{f_n(x)}, x ∈ [a; b], f_n(x) ∈ C([a; b])

∀ x ∈ [a; b] ∃  f_n(x) = f(x).

Будет функция f(x) непрерывной на [a; b]?

Ответ

Отрицательный