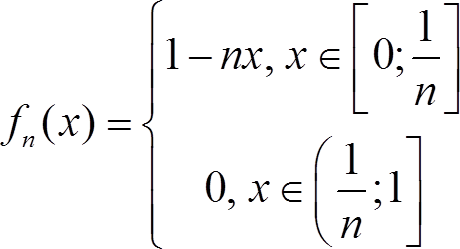Равномерная сходимость функциональной последовательности

Пример

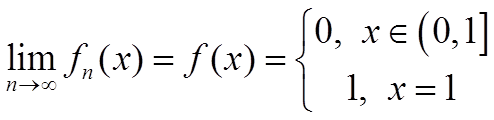— устранимый разрыв.

Последовательность f_n(x) непрерывных функций на отрезке [a; b] сходится к функции f(x) равномерно, если

∀ ε > 0 ∃ N = N(ε): ∀ x ∈ [a; b], ∀ n > N → |f_n(x) − f(x)| < ε

Критерий: Последовательность бесконечно малая.

Теорема

1)  f_n(x), x ∈ [a; b];

2){f_n(x)} — сходится равномерно.

Тогда f(x) — непрерывная функция на [a; b].