Теорема о нуле непрерывной функции
Теорема 4
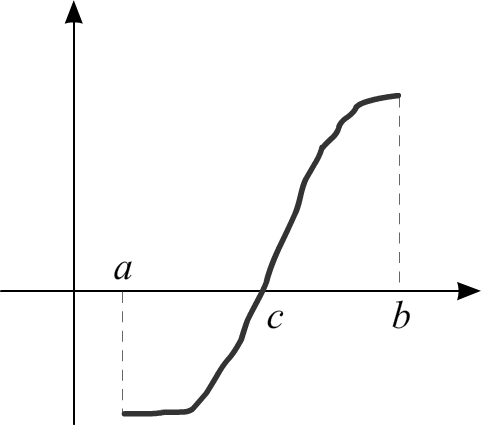
Пусть функция y = f(x) непрерывна на отрезке [a; b] и f(a) · f(b) < 0. Тогда существует точка c ∈ [a; b], для которой
f(c) = 0.
Доказательство
1) f(a1)·f(b1) < 0 2) f(a2)·f(b2) < 0 n) f(an)·f(bn) < 0 |
|
|
[a; b] ⊃ [a1; b1] ⊃ ... [an; bn] ⊃ ... → ∃ c ∈ [an; bn] ∀ n → f(c) = 0.
an ↑, an ≤ b → ∃ ![]() = c1, bn ↓, bn ≥ a → ∃
= c1, bn ↓, bn ≥ a → ∃ ![]() = c2
= c2