Определение производной. Производная и дифференциал

Доказательство

Пусть функция имеет производную f ′(a), тогда

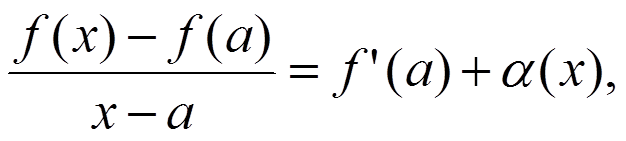
где α(x) — функция, имеющая при x → a предел, равный нулю. Из этого равенства находим

f(x) − f(a) = f′(a)(x − a) + α(x)(x − a),

что доказывает дифференцируемость функции с постоянной A = f ′(a).

Обратно, пусть функция дифференцируема, тогда

f(x) − f(a) = A(x − a) + α(x)(x − a)

где α(x) — функция, имеющая при x → a предел, равный нулю. Из этого соотношения получаем, что

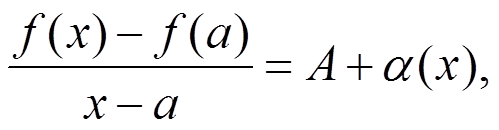
и в силу арифметических свойств предела

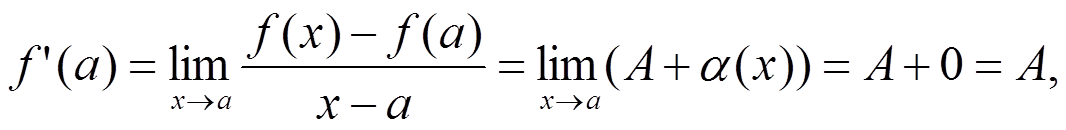
т. е. производная функции существует и равна A.