Основные правила вычисления производных

Так как функция t = φ(x) дифференцируема в точке x = x₀, то она непрерывна в этой точке. Функцию α(t) можно считать непрерывной в точке t = t₀ = φ(x₀). По теореме о непрерывности сложной функции α(φ(x)) непрерывна при x = x₀, т. е.

Но тогда

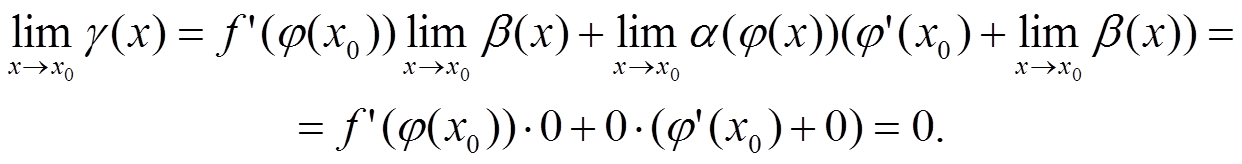
Итак

F(x) − F(x₀) = A(x − x₀) + γ(x)(x − x₀),

где A = f ′(φ(x₀))φ′(x₀), и

Отсюда следует, что функция

F(x) = f(φ(x))

дифференцируема в точке x = x₀, и её производная

F ′(x₀) = A = f ′(φ(x₀))φ′(x₀).