Основные правила вычисления производных

Производная обратной функции

Пусть функция

y = f(x)

монотонна и непрерывна в окрестности точки x₀, в самой точке x₀ существует производная, которая не равна нулю. Тогда обратная функция

x = g(y)

также имеет производную в точке

y₀ = f(x₀)

и

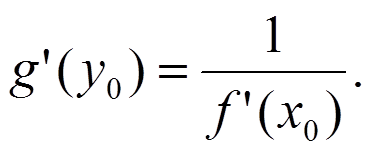
Доказательство

Из условий теоремы вытекает непрерывность обратной функции, поэтому при y → y₀ величина x → x₀. Положим

y = f(x)

и учтём, что при этом

y₀ = f(x₀), x = g(y), x₀ = g(y₀).

Тогда

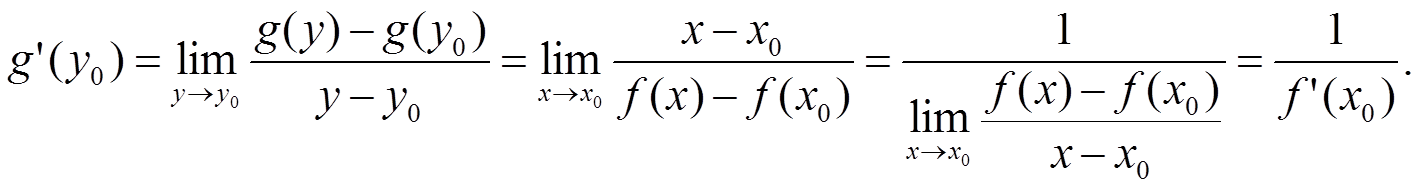
Это доказывает утверждение теоремы.