Теорема Ферма

2. Пусть функция f(x) имеет в точке x₀ минимум. Тогда у этой точки существует окрестность, в которой f(x) ≥ f(x₀). В этом случае при x < x₀ мы имеем неравенство

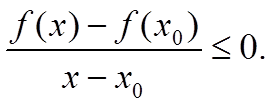
Переходя в этом неравенстве к пределу, получаем, что f ′(x₀) ≤ 0.

С другой стороны, при x < x₀ мы имеем неравенство

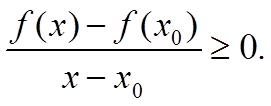
Переходя к пределу в этом неравенстве, получаем, что f ′(x₀) ≥ 0. Отсюда следует, что f ′(x₀) = 0.

Теорему Ферма часто называют необходимым условием экстремума. Если функция имеет экстремум во внутренней точке и производная функции в этой точке существует, то эта производная должна быть равна нулю.