Производная сложной функции

Aβ(z))|z − a| = o(|z − a|).

Лемма

Справедливо неравенство

|Ax| ≤ M(A)|x|, где M(A) =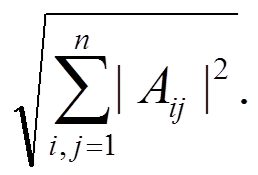

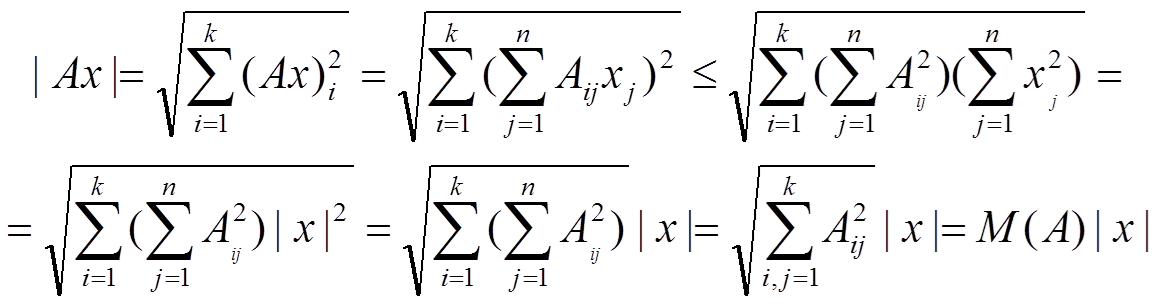
|Aβ(z)| ≤ M(A) | β(z)| ⇒ Aβ(z) → 0 при z → a

a(g(z))|g(z) − g(a)| = o(|z − a|).

g(z) − g(a) = B(z − a) + β(z)|z − a|,  

|g(z) − g(a)| = |B(z − a) + β(z)|z − a|| ≤

≤ |B(z − a) + β(z)||z − a| ≤

≤ M(B)|z − a| + |β(z)||z − a| =

= [M(B) + |β(z)|]| z − a | = O(|z − a|)

a(g(z))|g(z) − g(a)| = o(|z − a|).