Непрерывность векторной функции

Векторная функция (вектор-функция)

f(x) = f₁(x), f₂(x), ..., f_m(x)),   x ∈ Rⁿ, f(x) ∈ R^m,

(подразумевается, что все координатные функции имеют общую область определения, которая и является областью определения векторной функции)

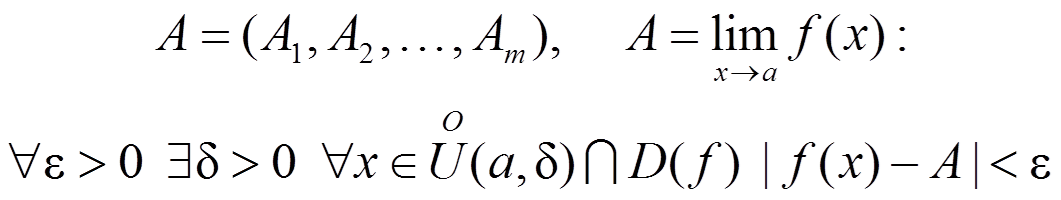
(a — предельная точка области определения функции).

1) Для любой последовательности x_k, лежащей в области определения f(x) и сходящейся к a, последовательность значений функции f(x_k) сходится к f(a).

2) Для любого ε > 0 существует такое δ > 0, что для всех точек, лежащих в U(a, δ) ∩ D(f) выполняет неравенство
|f(x) − f(a)| < ε.

f(x) непрерывна в точке a ⇔ все функции f₁(x), f₂(x), ..., f_m(x) непрерывны в точке a.