Достаточное условие экстремума
f ∈ C2(Ω), a ∈ Ω, df(a) = 0.
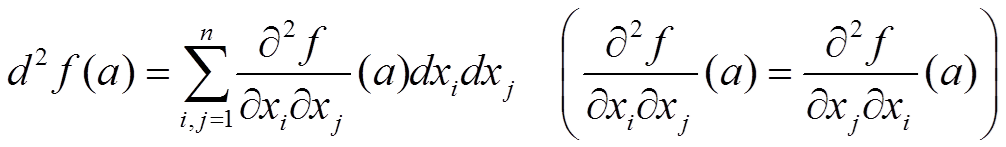
(второй дифференциал — квадратичная форма от ξ = dx)
Теорема
Пусть f ∈ C2(Ω), а — стационарная точка f, лежащая в Ω. Если d2f(a) положительно определённая форма, то x = a — точка минимума f, если d2f(a) отрицательно определённая форма, то x = a — точка максимума f.
Рассмотрим случай, когда второй дифференциал представляет положительно определённую форму. Пусть
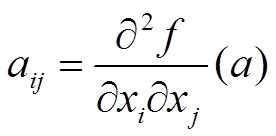
Рассмотрим функцию
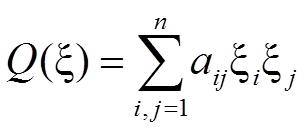
на единичной сфере
S = {ξ ∈ Rn: |ξ| = 1}.



