Достаточное условие экстремума

Так как

то

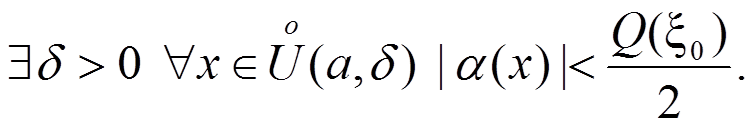
Поэтому

Но это и означает, что x = a является точкой строгого минимума.

Рассмотрим случай, когда второй дифференциал представляет отрицательно определённую форму.

Пусть

g(x) = −f(x)

dg(a) = −df(a) = 0,   d²g(a) = −d²f(a)

Следовательно, точка x = a является стационарной точкой g(x), причём второй дифференциал g(x) в точке x = a положительно определён. Отсюда следует, что g(x) имеет в точке x = a строгий минимум, поэтому функция f(x) = −g(x) имеет при x = a строгий максимум.