Примеры разложения дроби на элементарные

1871

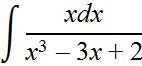
Разложение знаменателя подынтегральной функции на множители имеет вид x³ – 3x + 2 = (x – 1)²(x + 2). Равенство

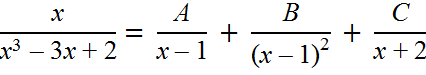
даёт

x = A(x − 1)(x + 2) + B(x + 2) + C(x − 1)².

Полагая x = 1, x = −2, получаем 1 = 3B, −2 = 9C, откуда B = 1/3, С = –2/9. Полагая x = 0, находим 0 = −2A + 2B + C, следовательно, A = (2B + C)/2 = 2/9. Из расположения

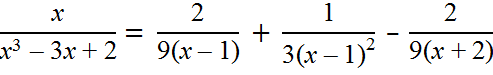
получаем

.
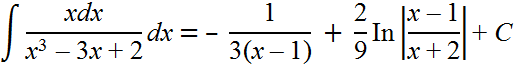