Разложение дроби на элементарные

Доказательство

Рассмотрим разность

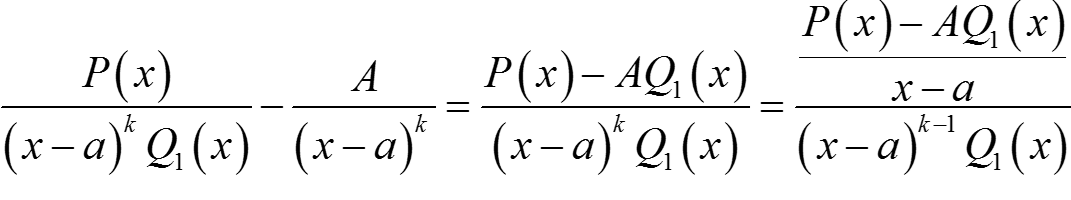
Если мы докажем, что P(x) − AQ₁(x) делится на x − a. То теорема будет доказана.

Докажем, что константу A можно подобрать так, что P(x) − AQ₁(x) будет делиться на x − a.

Положим x = a, тогда 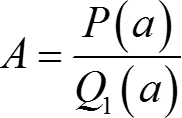⇒ A существует.

Покажем, что A определенно однозначно. Пусть существуют две константы A₁ и A₂. Тогда

P(x) − A₁Q₁(x) = (x − a)P₁(x) и

P(x) − A₂Q₁(x) = (x − a)P₂(x).

Вычитая из первого уравнения второе, получим

(−A₁ + A₂)Q₁(x) = (x − a)(P₁(x) − P₂(x)).

Подставим x = a:

(A₁ − A₂)Q₁(a) = 0 ⇒ A₁ − A₂ = 0 ⇒ A₁ = A₂ т. к. Q₁(a) ≠ 0.