Интегрирование тригонометрических функций

I. Пусть функция R(u, v) меняет знак при изменении знака u. Тогда, согласно свойству 2

∫R(sin x, cos x)dx = ∫R₂(sin² x, cos x)sin xdx = −∫R₂(1 − cos² x, cos x)d cos x = −∫R₂(1 − t², t)dt,

где t = cos x.

II. Пусть R(u, v) меняет знак при изменении знака v. Тогда

∫R(sin x, cos x)dx = ∫R₃(sin x, cos² x)cos xdx = ∫R₃(sin x, 1 − sin² x)d sin x = ∫R₃(t, 1 − t²)dt,

где t = sin x.

III. Пусть функция R(u, v) не меняет своего значения при одновременном изменении знака u и v, т. е. R(u, v) = R(−u, −v). Докажем, что в этом случае интеграл от функции R(sin x, cos x) рационализируется подстановкой t = tg x.

, ,

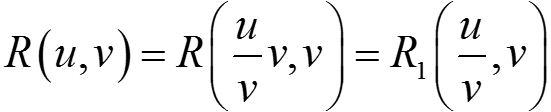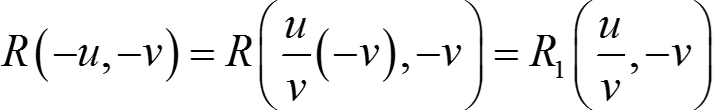т. о.

⇒ ⇒ ⇒

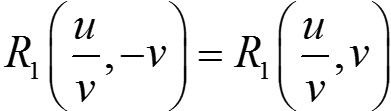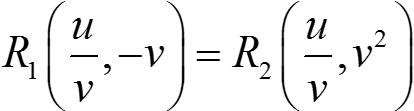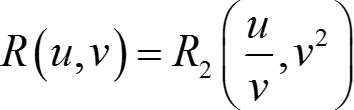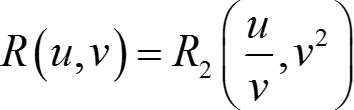⇒ ∫R(sin x, cos x)dx = ∫R₂(tg x, cos² x)dx =

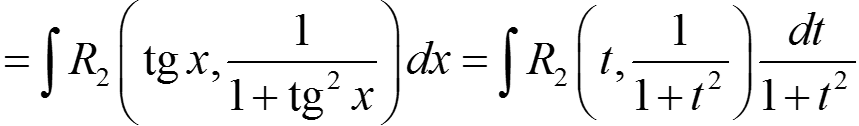, где t = tg x, x = arctg t, .