Теоремы о среднем для интеграла Римана

Теорема 1

Пусть функции f(x), (x) непрерывны на [a; b] и (x) ≥ 0. Тогда существует точка c ∈ [a; b], для которой

f(x)(x)dx = f(c)(x)dx.

Доказательство

E_f = [m; M]. Тогда

m(x)dx ≤ f(x)(x)dx ≤ M(x)dx.

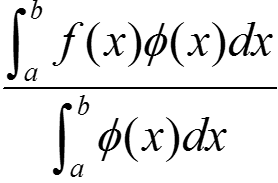∈ [m; M] и ∃ c ∈ [a; b] → 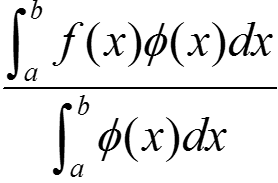= f(c).