Теоремы о среднем для интеграла Римана

Теорема 2

Функция f(x) непрерывна на [a; b] функция φ(x) — непрерывна на [a; b] и имеет производную на (a; b), причём φ ′ (x) ≤ 0. Тогда существует c ∈ [a; b], для которой

I = f(x)φ(x)dx = φ(a)·f(x)dx.

Доказательство

Пусть F(x) = f(t)dt — первообразная, тогда

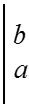I = φ(x)dF(x) = φ(x)·F(x) − φ′(x)F(x)dx =

= φ(b)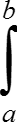 f(x)dx + 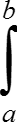(−φ′(x))F(x)dx.

Пусть E_f = [m; M], тогда из условия −φ′(x) ≥ 0 следует

m(φ(b)+ −φ′(x)dx) ≤ I ≤M(φ(b)+ −φ′(x)dx) →

→ m(φ(a) ≤ I ≤ M(φ(a) → ·I ∈ [m; M] → ∃ c ∈ [a; b]: F(c) = I →

I = φ(a)·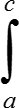f(x)dx.

Аналог теоремы 2

Если φ(x) ≥ 0 и φ′(x) ≥ 0 ∀ x ∈ [a; b], то ∃ c ∈ [a; b]: 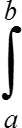f(x)φ(x)dx = φ(b)·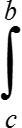f(x)dx.