Интеграл с переменным верхним пределом
Доказательство
∀ c ∈ (a, b)
F(x) − F(c) = f(c)(x − c) +
+ 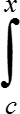 (f(t) − f(c))dt = f(c)(x − c) + φ(x, c)·(x − c),
(f(t) − f(c))dt = f(c)(x − c) + φ(x, c)·(x − c),
где 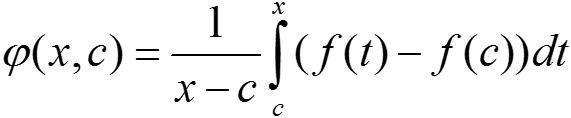 .
.
Докажем, что φ(x, c) — бесконечно малая функция в точке x = c.
![]() .
.
Тогда
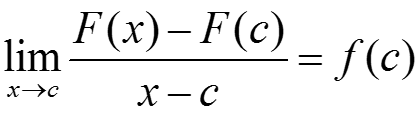 .
.
Доказательство
∀ c ∈ (a, b)
F(x) − F(c) = f(c)(x − c) +
+ 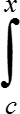 (f(t) − f(c))dt = f(c)(x − c) + φ(x, c)·(x − c),
(f(t) − f(c))dt = f(c)(x − c) + φ(x, c)·(x − c),
где 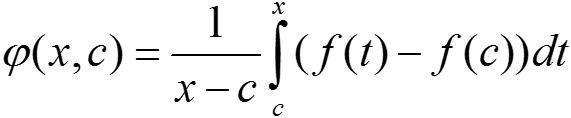 .
.
Докажем, что φ(x, c) — бесконечно малая функция в точке x = c.
![]() .
.
Тогда
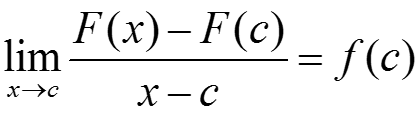 .
.