Признаки абсолютной сходимости для несобственных интегралов первого рода

2) p ≠ 1. В этом случае первообразная подынтегральной функции

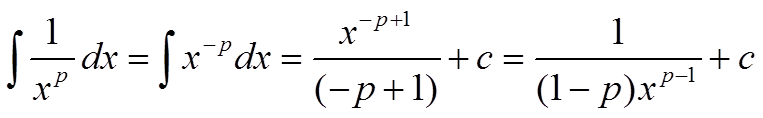
При стремлении верхнего предела к бесконечности предел

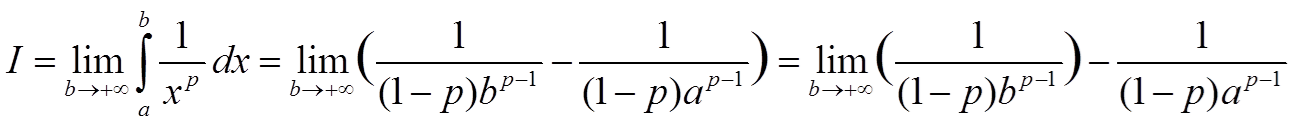
при p < 1 равен бесконечности, то есть интеграл расходится.

Предел отношения

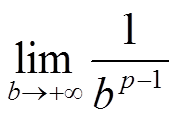
равен нулю, если знаменатель возводим в положительную степень (то есть p − 1 > 0, или p > 1), и равен бесконечности, если возводим в отрицательную степень (то есть p − 1 < 0, или p < 1 ).

Ответ

Если p > 1, то несобственный интеграл первого рода

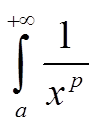dx, a > 0

сходится. Если p ≤ 1, то несобственный интеграл первого рода расходится.