Частный признак сравнения для несобственных интегралов первого рода

Теорема 3

Пусть на полупрямой a < x < +∞ функция f(x) удовлетворяет условию

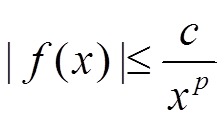
где c, p — постоянные, p > 1, тогда интеграл

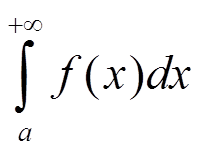
сходится абсолютно.

Если существуют постоянные c > 0, p ≤ 1, такие что на полупрямой 0 < a < x < +∞ функция f(x) удовлетворяет условию

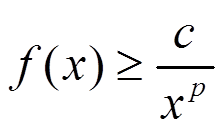
то интеграл

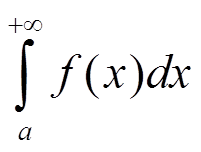
расходится.