Частный признак сравнения для несобственных интегралов первого рода

Доказательство

Доказательство следует из общего признака сравнения и примера 4, необходимо положить

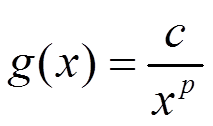
Следствие теоремы 3

Если функция f(x) эквивалентна

f(x) ∼ 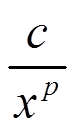при x → +∞

то при p > 1, интеграл

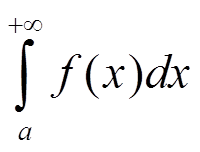
сходится, а при p ≤ 1, интеграл расходится.