Критерий Коши сходимости несобственного интеграла второго рода

Для сходимости несобственного интеграла второго рода необходимо и достаточно, чтобы

∀ ε > 0 ∃ δ = δ(ε) > 0: ∀ α₁, ∀ α₂, 0 < α₂ < α₁ < δ ⇒ 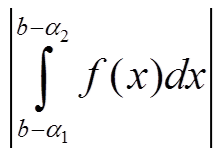< ε

Доказательство

По определению несобственный интеграл (2) сходится тогда и только тогда, когда существует конечный предел функции

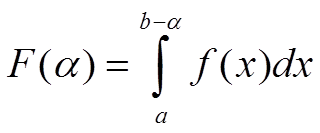при α → +0

По критерию Коши существования конечного предела функции необходимо и достаточно, чтобы

∀ ε > 0 ∃ δ = δ(ε) > 0: ∀ α₁, ∀ α₂, 0 < α₂ < α₁ < δ ⇒ |F(α₁) − F(α₂)| < ε

По определению функции F(x)

|F(α₁) − F(α₂)| =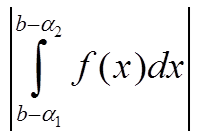

Критерий Коши доказан