Частный признак сравнения для несобственных интегралов второго рода

Следствие теоремы 4

Если функция f(x) эквивалентна

f(x) ∼ 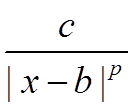при x → b, c ≠ 0

то интеграл для исходной функции и интеграл для эквивалентной функции сходятся и расходятся одновременно.

А именно, несобственный интеграл второго рода

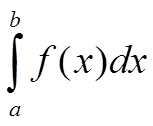
сходится при p < 1,

расходится при p ≥ 1.