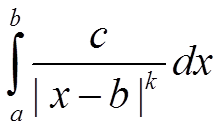Частный признак сравнения для несобственных интегралов второго рода

Доказательство

Вспомним определение эквивалентных функций. Две функции f(x) и g(x) называются эквивалентными при

f(x) ∼ g(x) при x → b

если найдётся такая новая функция h(x), что

f(x) = g(x)h(x),   lim h(x) = 1 при x → b

Запишем определение, что предел функции h(x) равен 1:

∀ ε > 0 ∃ δ > 0: ∀ x ∈ (b − δ, b) ⇒ |h(x) − 1| < ε

1 − ε < h(x) < 1 + ε

ε = 0,5;   0,5 < h(x) < 1,5

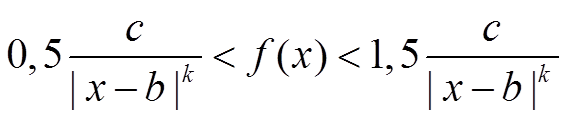
Из этого двойного неравенства следует, что интеграл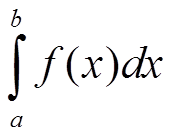

сходится или расходится одновременно с интегралом функции