Абсолютная и условная сходимость
Утверждение 1
Если интеграл
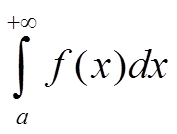
абсолютно сходится, то он является сходящимся.
Доказательство
Дано
Интеграл
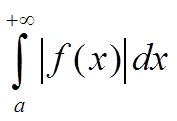
сходится, тогда по критерию Коши
∀ ε > 0 ∃ b = b(ε) > a: ∀ b′ > b, ∀ b′′ > b ⇒ 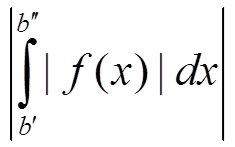 < ε
< ε

 Сходимость условная и абсолютная. Признаки сходимости
Сходимость условная и абсолютная. Признаки сходимости  Абсолютная и условная сходимость
Абсолютная и условная сходимостьУтверждение 1
Если интеграл
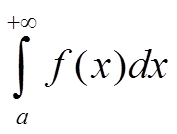
абсолютно сходится, то он является сходящимся.
Доказательство
Дано
Интеграл
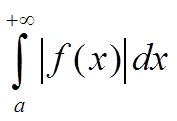
сходится, тогда по критерию Коши
∀ ε > 0 ∃ b = b(ε) > a: ∀ b′ > b, ∀ b′′ > b ⇒ 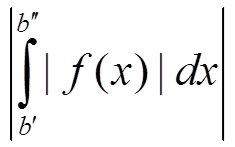 < ε
< ε