Абсолютная и условная сходимость
Тогда по свойствам неравенств верно, что
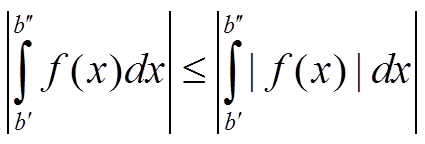
Тогда
∀ ε > 0 ∃ b = b(ε) > a: ∀ b′ > b, ∀ b′′ > b ⇒ 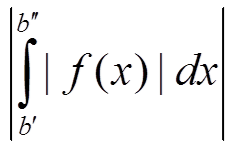 < ε
< ε
что по критерию Коши означает, что интеграл
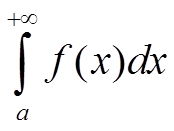
сходится.

 Сходимость условная и абсолютная. Признаки сходимости
Сходимость условная и абсолютная. Признаки сходимости  Абсолютная и условная сходимость
Абсолютная и условная сходимостьТогда по свойствам неравенств верно, что
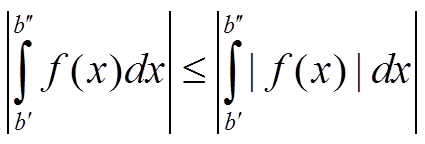
Тогда
∀ ε > 0 ∃ b = b(ε) > a: ∀ b′ > b, ∀ b′′ > b ⇒ 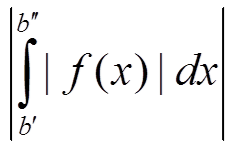 < ε
< ε
что по критерию Коши означает, что интеграл
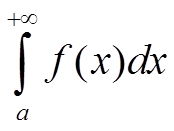
сходится.