Признак Дирихле–Абеля

Теорема 4

Признак Дирихле–Абеля

Пусть

1) функции f(x), g(x) определены на полупрямой [a, +∞] и для любого R > a существует определённый интеграл ,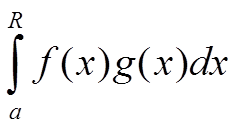

2) f(x) непрерывна на [a, +∞] и имеет на [a, +∞] ограниченную первообразную F(x),

3) функция g(x) монотонно не возрастает на полупрямой [a, +∞],

4) функция g(x) стремится к 0 при x, стремящемся к бесконечности,

5) функция g(x) имеет непрерывную производную g′(x) на [a,+∞], тогда сходится интеграл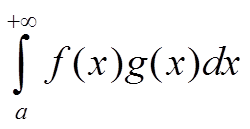.