Признак Дирихле–Абеля

Доказательство

По Критерию Коши интеграл

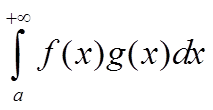
сходится тогда и только тогда, когда

∀ ε > 0 ∃ b = b(ε) > a: ∀ b′ > b, ∀ b′′ > b ⇒ 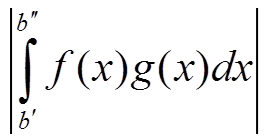< ε

Интеграл, записанный под модулем, преобразуем по формуле интегрирования по частям

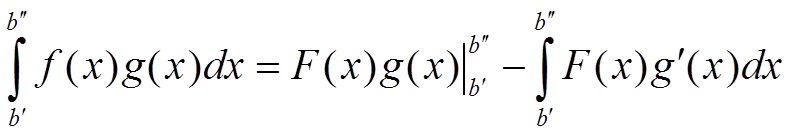
Так как F(x) — ограниченная функция

∃ K: ∀ x ∈ [a, + ∞) ⇒ |F(x)| < K

Так как функция g(x) монотонно не возрастает на полупрямой [a, +∞] и стремится к 0, то

g(x) ≥ 0, g′(x) ≤ 0