Признак Дирихле–Абеля

Тогда для интеграла верны оценки:

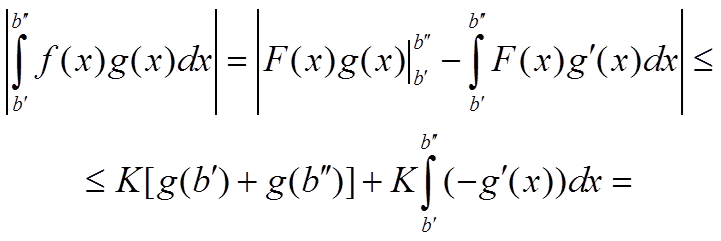
= K[g(b′) + (g(b′′)] + K(g(b′) − (g(b′′)) ≤ 2Kg(b′)

Вернёмся к критерию Коши. Возьмём произвольное ε > 0. Так как g(x) стремится к 0 при x, стремящемся к 0, то

∀ ε > 0 ∃ b: ∀ b′ ≥ b, верно g(b′) <

Тогда

∀ ε > 0 ∃ b: ∀ b′ ≥ b, ∀ b′′ ≥ b верно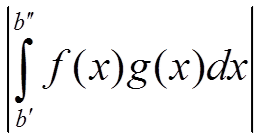 < ε

что и означает сходимость исходного интеграла.

Теорема доказана