Примеры

Рассмотрим интеграл из модулей.

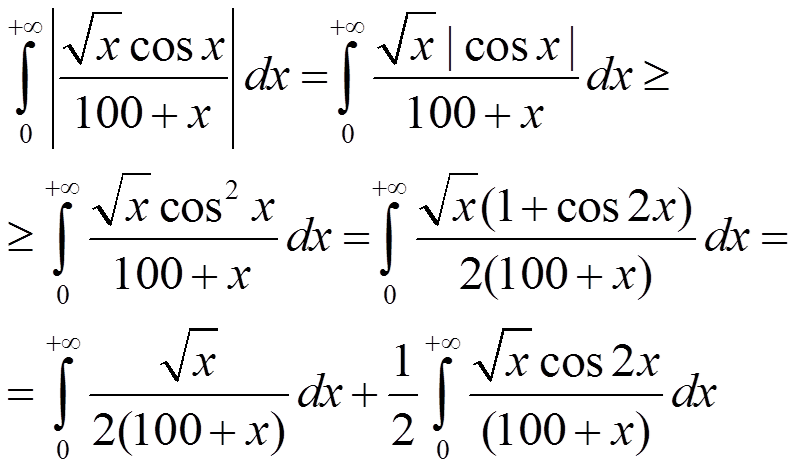
Второй из полученных интегралов сходится по признаку Дирихле–Абеля, а первый расходится по признаку сравнения со степенной функцией на бесконечности. Сумма сходящегося и расходящегося интеграла расходится. Следовательно, интеграл из модулей расходится, то есть несобственный интеграл первого рода сходится условно.

Ответ

Несобственный интеграл сходится условно.