Примеры

Пример

Исследовать на абсолютную и условную сходимость интеграл

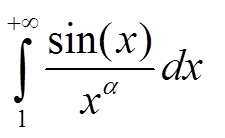
Решение

Положим

f(x) = sin(x), g(x) =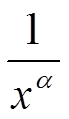

Тогда, видим, что при α > 0

F(x) = −cos(x), ∀ x ∈ R|F(x)| ≤ 1, g(x)0

Условия признака Дирихле–Абеля выполнены, интеграл сходится.

Исследуем на абсолютную сходимость. Так как |sin(x)| ≤ 1 для ∀ x ∈ R

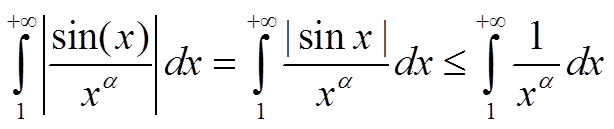
По признаку сходимости для степенной функции при α > 1 интеграл сходится абсолютно.

Рассмотрим

0 < α ≤ 1

Покажем, что интеграл из модулей расходится.