Примеры

2 случай

p − 1 < 0

Подынтегральная функция неограниченно возрастает в окрестности x = 0, если p < 1.

Разобьём промежуток интегрирования на два

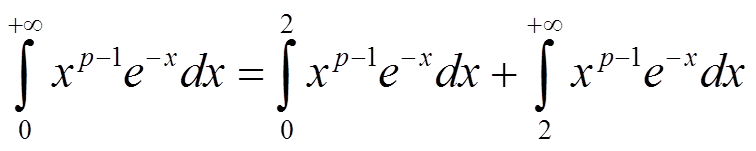
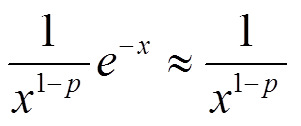при x → 1

В первом интеграле экспонента ограничена и не обращается в 0, по признаку сравнения несобственный интеграл второго рода сходится, если степень знаменателя 1 − p < 1 или p > 0.

Второй интеграл сходится, так как при p < 1 степенная функция на бесконечности стремится к 0, то есть ограничена на множестве (2, +∞), а интеграл от экспоненты сходится.

Ответ

Интеграл сходится при p > 0.