Примеры

2363

Исследовать сходимость интеграла

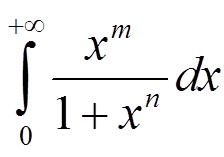, (n ≥ 0)

Решение № 2363

Разобьём интеграл на два, чтобы анализировать сходимость в окрестности 0 и окрестности бесконечности.

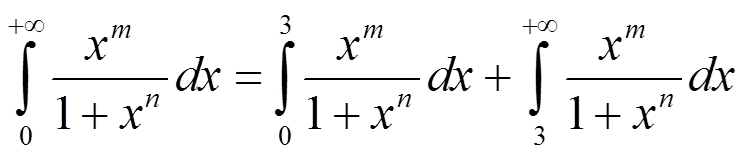
Рассмотрим первый интеграл. Так как n > 0, то знаменатель стремится к 1, подынтегральная функция эквивалентна

f(x) = 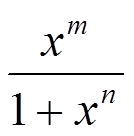≈ x^m, при x → 0

тогда несобственный интеграл второго рода сходится при m > −1.

Рассмотрим второй интеграл в окрестности бесконечности.

Так как n > 0, то подынтегральная функция эквивалентна

f(x) = 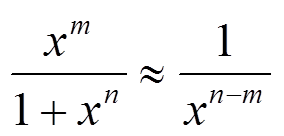, при x → +∞

тогда несобственный интеграл первого рода сходится при n − m > 1.

Ответ

Интеграл сходится при m > −1, n − m > 1. При остальных значениях параметров интеграл расходится.