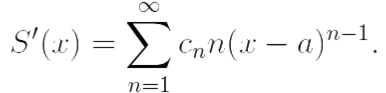Теорема о почленном дифференцировании

Доказательство

Аналогично доказательству теоремы о почленном интегрировании, так как ряд

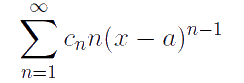
является степенным, то его радиус сходимости R' можно найти по формуле Коши–Адамара:

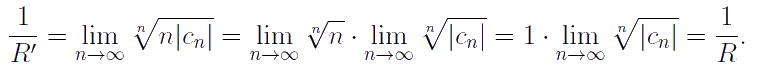
Таким образом, радиус сходимости ряда не меняется при дифференцировании:

R' = R.

Как степенной ряд сходится сходится равномерно на [a − r, a + r] при произвольном r ∈ (0, R).

Поскольку для любого x ∈ (a − R, a + R) найдётся r такой, что

x ∈ [a − r, a + r] ⊂ (a − R, a + R)

то по теореме о почленном дифференцировании равномерно сходящегося ряда получим, что в каждой точкеx ∈ (a − R, a + R) имеет место равенство