Степенной ряд. Теорема Коши-Адамара
Доказательство
Рассмотрим произвольную точку x ∈ (a −R, a + R) и обозначим |x − a| = r. Тогда r < R, a так как 
то начиная с некоторого номера N ∈ 
,
∃ q ∈ (0, 1): ∀ n > N 
Следовательно, степенной ряд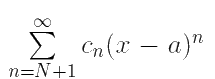
мажорируется числовым рядом
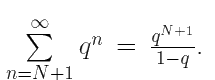(Данный числовой ряд сходится по признаку Коши, поскольку q ∈ (0, 1).)
В силу I-го признака сравнения, ряд 
сходится в рассматриваемой точке x. А поскольку мы рассматривали произвольную точку x ∈ (a − R, a + R), то степенной ряд 
сходится всюду в (a − R, a + R). Отсюда и весь ряд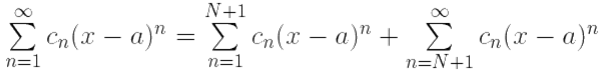 
сходится абсолютно всюду в (a − R, a + R).
Теперь надо доказать, что во всех точках x: |x − a| > R, ряд расходится.
Фиксируем произвольную точку x такую, что |x − a| > R. Так как
то начиная с некоторого номера N ∈ ,
⇒ сn (x − a)n 
0 при |x − a| > R.
Получаем, что для |x − a| > R не выполнено необходимое условие сходимости ряда 
следовательно, он рассходится при всех x: |x − a| > R.
