Степенной ряд. Теорема Коши-Адамара

Пример

Рассмотрим ряд Исследуем его сходимость. Здесь По формуле из замечания имеем:

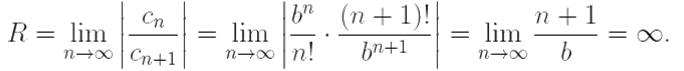
Таким образом, ряд сходится абсолютно на (−∞, +∞).

Пример

Рассмотрим ряд Исследуем его сходимость. По формуле Коши–Адамара имеем

∀ p ∈ . Таким образом, ряд сходится абсолютно на (−1, 1) и расходится при | x | > 1.

Осталось исследовать точки |x| = 1.

В точке |x| = −1 ряд превращается в числовой ряд вида:При p ≥ 0 нарушается необходимое условие сходимости числового ряда (общий член не стремиться к нулю), поэтому ряд расходится. При p < 0 наш числовой ряд представляет собой ряд Лейбница, следовательно, сходится, причём при p < −1 он сходится абсолютно (по интегральному признаку).

В точке  x = 1 ряд превращается в числовой ряд вида: По интегральному признаку, при p ≥ −1 ряд расходится, а при p < −1 сходится.