Теорема о почленном интегрировании

Теорема

Почленное интегрирование

Условие

R — радиус сходимости степенного ряда

Утверждение

∀ r ∈ (0, R)   S(x) интегрируема по Риману на [a − r, a + r] и ∀ [a, β] ⊂ (a − r, a + r).

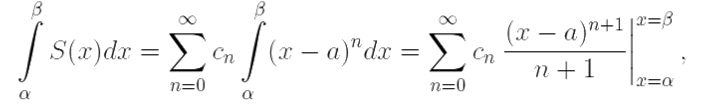
то есть степенной ряд можно почленно интегрировать.

В частности, если взять x ∈ (a, a + R) и проинтегрировать ряд по промежутку [a, x], по свойству интеграла с переменным верхним пределом получим

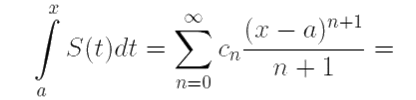
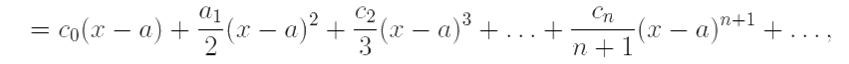
при этом полученный ряд имеет тот же радиус сходимости R.