Теорема о почленном интегрировании

Доказательство

В силу первого из доказанных свойств степенного ряда, исходный ряд сходится равномерно на [a − r, a + r] при произвольном
R ∈ (0, R). Поэтому для любого x ∈ (a, a + R) этот ряд равномерно сходится на [a, x]. Применим теорему о почленном интегрировании равномерно сходящегося ряда и получим, что имеют место требуемые равенства.

Так как ряд

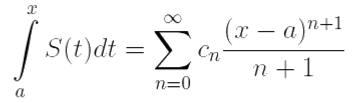
является степенным, то его радиус сходимости R_f  можно найти по формуле Коши–Адамара:

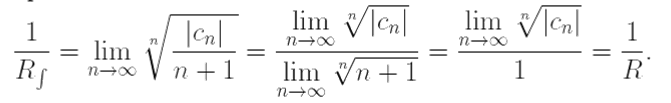
Таким образом, радиус сходимости ряда не меняется при интегрировании:

R_f = R.