Таблица разложений элементарных функций

Пример

Разложить в степенной ряд функцию f(x) = cos x.

Поскольку

(cos x)' = −sin x, (cos x)'' = −cos x,

(cos x)⁽³⁾ = sin x, (cos x)⁽⁴⁾ = cos x, ...

То при x = 0 получим

при n = 0, 4, 8, ... при n = 2, 6, 10, ... при n = 1, 3, 5, ...

Таким образом, все коэффициенты с нечётными номерами обращаются в нуль, а с чётными — в ±1, причём их знаки чередуются. Поэтому, по определению ряда Тейлора:

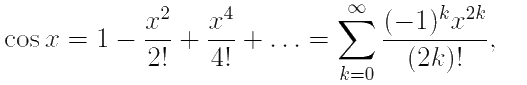   x ∈ (−∞, +∞);    

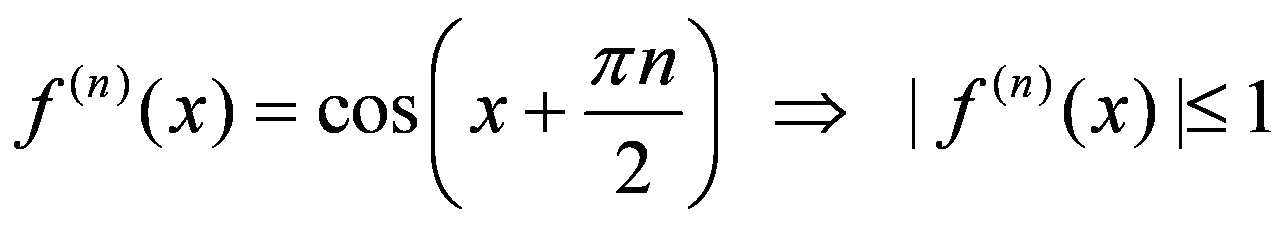
 (в любом интервале x ∈ (−δ, +δ))

Отсюда следует, что наша функция раскладывается в ряд Тейлора в любом интервале, т. е. на всей числовой прямой.