Таблица разложений элементарных функций

Пример

Разложить в степенной ряд функцию f(x) = ln (1 + x).

Заметим, что

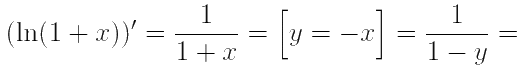
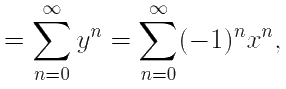      | x | < 1.

Проигнорируем равенство

По промежутку t ∈ [0, x] при |x| < 1 (т. е. по интервалу, на котором это равенство имеет место):

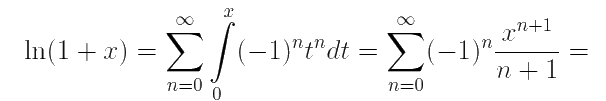
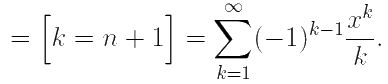
Таким образом, мы получили в точности то разложение, которое приведено выше. (Поскольку

∀ k ∈    (−1) ^(k+1) = (−1)^k−1).

(Здесь применение достаточного условия не нужно, разложение функции в ряд следует из теоремы о почленном интегрировании степенных рядов)