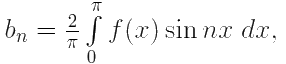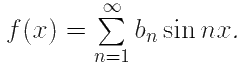Ряд Фурье от чётной и нечётной функции

Напомним понятия чётной и нечётной функции. Пусть функция f(x) определена на симметричном относительно точки 0 множестве X. Это означает, что если точка x принадлежит множеству X, то и точка −x ∈ X.

Определение

Функция f(x), определённая на симметричном относительно нуля множестве X, называется чётной, если

∀ х ∈ f(−x) = f(x)

Функция f(x), определённая на симметричном относительно нуля множестве X, называется нечётной, если

∀ х ∈ f(−x) = −f(x)

При этом график чётной функции симметричен относительно оси Oy, а график нечётной функции симметричен относительно точки O(0, 0).

Утверждение

1) f(x) ∈ QC[−π, π] — чётная на [−π, π] функция ⇒

b_n = 0,   

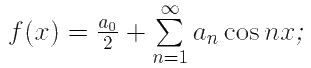
2) f(x) ∈ QC[−π, π] — нечётная на [−π, π] функция ⇒

a_n = 0,