Теорема о сумме ряда Фурье

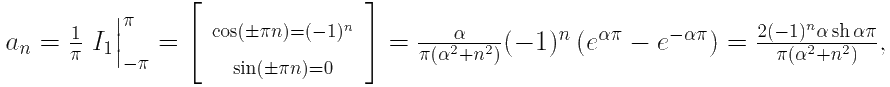
Теперь найдём a_n и b_n:

n ∈ .

Важно заметить, что коэффициент a₀ всегда надо искать отдельно:

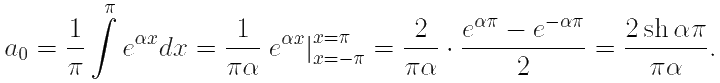
В результате для функции f(x) = e^αx на отрезке [−π, π] по формуле

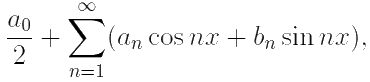
имеем разложение:

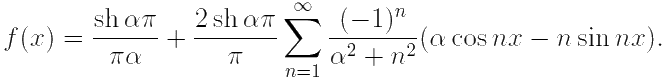
Поскольку по теореме о сумме ряда Фурье данный ряд внутри интервала (−π, π) сходится к функции f(x) = e^αx, а вне [−π, π] — к её периодическому продолжению F(x) с периодом 2π, то график суммы ряда Фурье — это график 2π-периодической функции, которая на промежутке (−π, π) совпадает с e^αx.