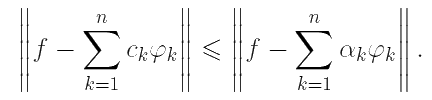Равенство Парсеваля
Определение
Гильбертово пространство Н называется сепарабельным, если в нём существует счётное всюду плотное множество.
Другими словами, пространство Н-сепарабельно, если в нём существует счётный базис — система элементов \(\left\{ \varphi_k \right\}_{k=1}^{\infty} \subset H\) такая, что любой элемент x ∈ H можно (и притом единственным образом) представить в виде ряда (разложить по базису):
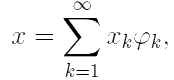xk ∈ 
Теорема
Пусть Н — сепарабельное гильбертово пространство, а
— полная ортонормированная система (ПОНС) элементов Н. Элементу f ∈ H его сопоставлен ряд Фурье с коэффициентами сk.
Тогда справедливо равенство Парсеваля:
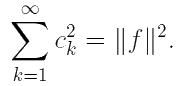
Доказательство
Поскольку система 
— полна в H, то по определению найдутся такие коэффициенты, \(\alpha_k\) ∈ , что
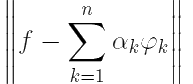→ 0 при n → ∞.
C другой стороны, в силу минимизирующего свойства ряда Фурье,
