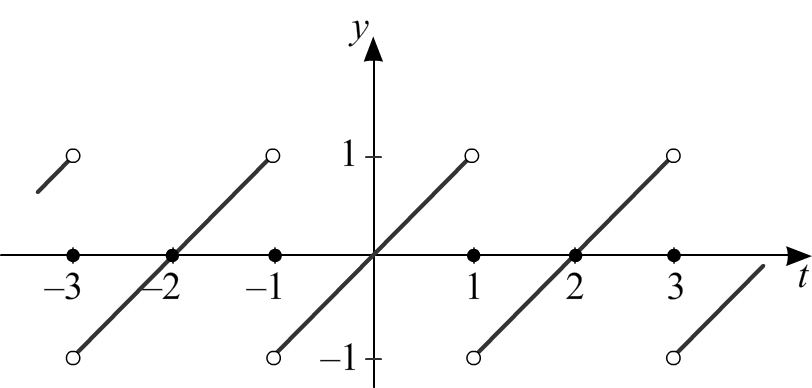
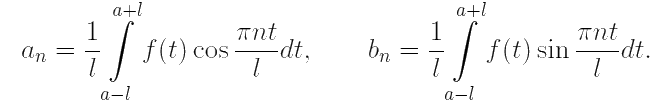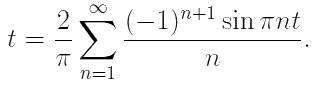Тригонометрический ряд Фурье на промежутке [– 1, 1]

Поэтому на промежутке [−1, 1] функция f(t) имеет разложение:

Замечание

Бывает необходимо представить функцию f(t) её рядом Фурье по произвольному промежутку [a − l, a + l], не симметричному относительно нуля, с заданными a ∈ и l > 0.

Эту задачу также решают при помощи замены переменных: если x меняется от (−π) до π, то будет меняться как раз в пределах от (a − l) до (a + l). В результате получим ряд Фурье общего вида

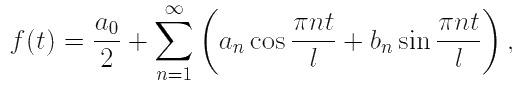t ∈ (a − l, a + l),

где коэффициенты находятся по формулам: