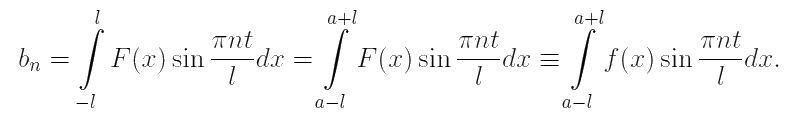Тригонометрический ряд Фурье на промежутке [– 1, 1]

Убедиться в справедливости этих формул можно и из геометрических соображений. Поскольку ряд Фурье функции f(x) сходится к её 2l-периодическому продолжения F(x), а множители

и

также являются 2l-периодическими функциями, то и произведения

и

обязаны быть 2l-периодическими функциями. Для 2l-периодических функций не имеет значения, по какому именно промежутку (если его длина равна периоду) ведётся интегрирование, следовательно, для промежутков (−l, l) и (a − l, a + l) ∀ a ∈  результат будет один и тот же: