Арифметические свойства сходящихся рядов

— Если 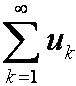сходится, и его сумма равна S, то 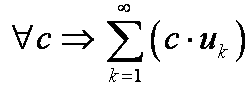также сходится, причём его сумма равна с · S.

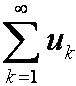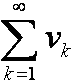— Если ряды и сходятся,  и их суммы равны соответственно S_u и S_v, то ряд также сходится, и его сумма S_u+v = S_u + S_v.

— Ряды 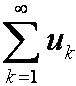и 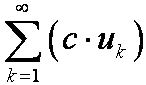, где с ≠ 0, сходятся и расходятся одновременно.

Доказательство

Доказательство этих утверждений основано на связи сходимости ряда со сходимостью последовательности (частичных сумм) и на арифметических свойствах предела последовательности. Рекомендуется выполнить в качестве упражнения.