Знакоположительные ряды. Критерий сходимости знакоположительного ряда
Рассмотрим ряд, все члены которого неотрицательны: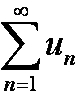 
: ∀ n ⇒ un ≥ 0. Такой ряд называется знакоположительным. Аналогично можно рассмотреть знакоотрицательный ряд, все члены которого неположительны. Оба типа рядов носят название знакопостоянных (знакоопределенных). Для таких рядов можно сформулировать особые признаки сходимости. Поскольку конечное число членов ряда не влияет на его сходимость, то логично считать ряд знакопостоянным, если его члены становятся неотрицательными (неположительными) хотя бы начиная с некоторого конечного номера N0. Далее будем рассматривать только знакоположительные ряды (знакоотрицательные сводятся к ним путем умножения на −1).
Для знакоположительных рядов имеется аналог теоремы о монотонных последовательностях.
Теорема
Ряд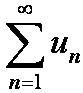 
с неотрицательными членами сходится ⇔ последовательность его частичных сумм 
ограничена сверху
(т. е. ∃ M > 0: ∀ n ⇒ Sn ≤ M).
Доказательство
|⇒| Пусть 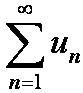сходится ⇒ ∃ конечный 
ограничена.
|⇐| Поскольку члены ряда неотрицательны, то ∀ n ⇒ Sn+1 = Sn + un+1 ≥ Sn ⇒ не убывает и, по условию, ограничена сверху ⇒ ∃ конечный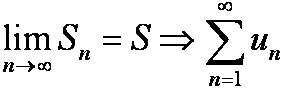 
сходится.
Замечание
Очевидно, что расходящийся знакоположительный числовой ряд всегда имеет сумму S, и S = +∞.
