Необходимое и достаточное условие сходимости ряда (Критерий Коши)

Следствие 3

Изменение конечного числа членов ряда 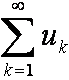не меняет его сходимости.

Доказательство

Пусть ряд 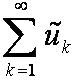. получен из 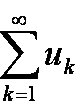изменением конечного числа членов. Тогда найдётся такой номер N₁, начиная с которого члены обоих рядов будут неразличимы.  Если 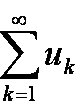сходится, для него будет выполнено  условие Коши, в котором N = N(ε). Тогда и для ряда 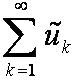оно точно будет выполнено, если  = max(N₁, N(ε)):

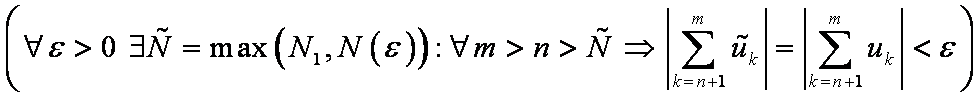⇔ ряд 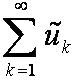сходится.

Замечание

Аналогично можно показать, что изменение конечного числа членов ряда 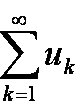не меняет его расходимости. Рекомендуется выполнить в качестве упражнения.